Coding

Table of Contents

• C++
• APIs
• Object-Oriented Design and Programming
• How to Test Your Code
• Corner Cases and Edge Cases

C++

Count the Repetitions

APIs

Read n Characters Given read4 II - Call Multiple Times

Given a file and assuming that you can only read the file using a given method read4, implement a method read to read n characters. Your method read may be called multiple times.

Method read4

The API read4 reads four consecutive characters from file, then writes those characters into the buffer array buf4. The return value is the number of actual characters read. read4() has its own file pointer, much like FILE *fp in C.

Definition of read4

Parameter: char[] buf4

Returns: int

buf4[] is a destination, not a source. The results from read4 will be copied to buf4[].

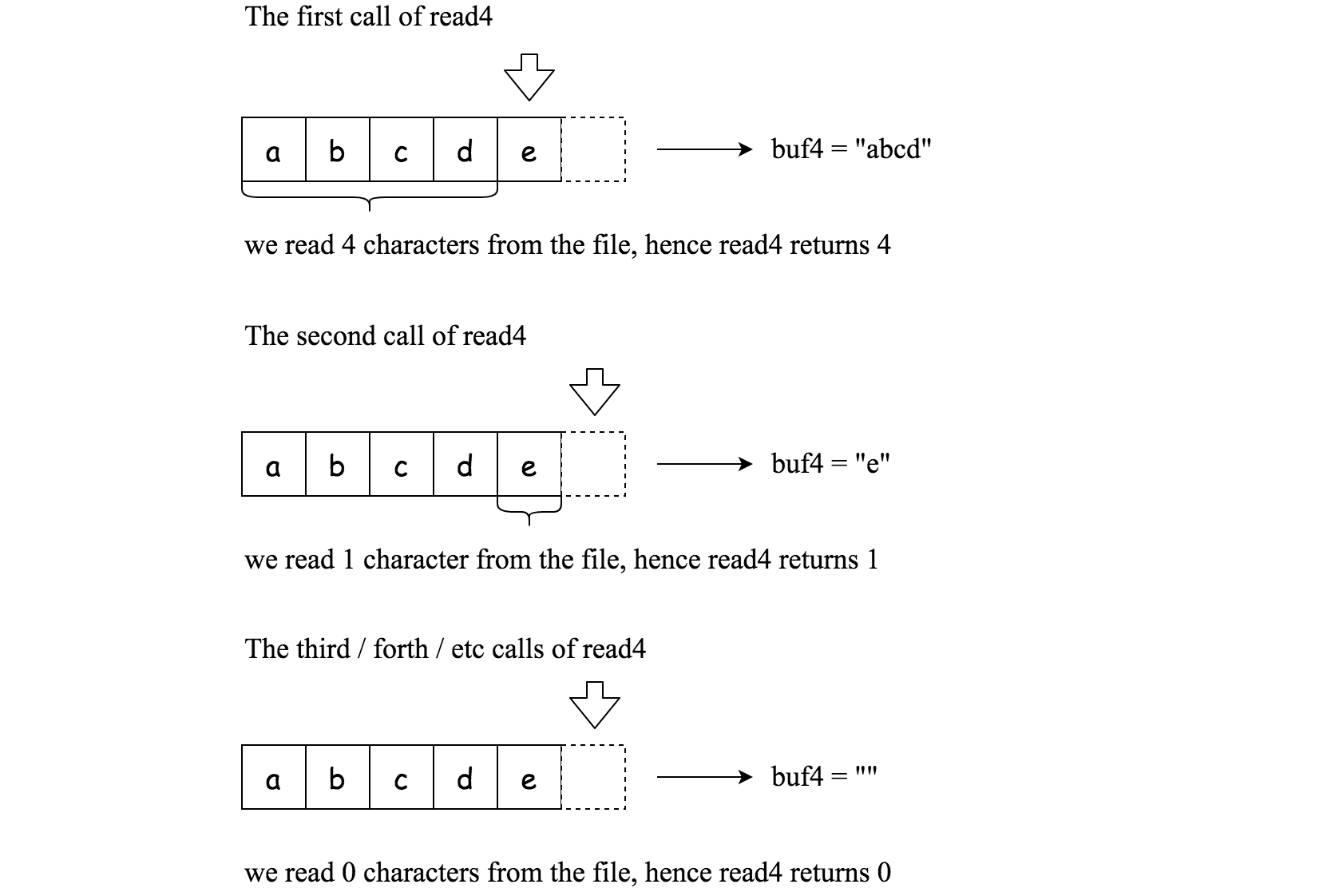
Below is a high-level example of how read4 works:

File file("abcde"); // File is "abcde", initially file pointer (fp) points to 'a'
char[] buf4 = new char[4]; // Create buffer with enough space to store characters
read4(buf4); // read4 returns 4. Now buf4 = "abcd", fp points to 'e'
read4(buf4); // read4 returns 1. Now buf4 = "e", fp points to end of file
read4(buf4); // read4 returns 0. Now buf4 = "", fp points to end of file

Method read

By using the read4 method, implement the method read that reads n characters from file and store it in the buffer array buf. Consider that you cannot manipulate file directly. The return value is the number of actual characters read.

Definition of read

Parameters: char[] buf, int n

Returns: int

buf[] is a destination, not a source. You will need to write the results to buf[].

Notes:

• Consider that you cannot manipulate the file directly. The file is only accessible for read4 but not for read.
• The read function may be called multiple times.
• You may assume the destination buffer array, buf, is guaranteed to have enough space for storing n characters.
• It is guaranteed that in a given test case the same buffer buf is called by read.

int i = 0, m = 0;
char buf4[4];

int read(char *buf, int n) {
    int j = 0;
    while (j < n) {
        if (!i) m = read4(buf4);
        if (!m) break;
        while (j < n && i < m) buf[j++] = buf4[i++];
        if (i >= m) i = 0;
    }
    return j;
}

Object-oriented Design and Programming

LFU Cache

Design and implement a data structure for a Least Frequently Used (LFU) cache. Implement the LFUCache class:

• LFUCache(int capacity) Initializes the object with the capacity of the data structure.
• int get(int key) Gets the value of the key if the key exists in the cache. Otherwise, returns -1.
• void put(int key, int value) Update the value of the key if present, or inserts the key if not already present. When the cache reaches its capacity, it should invalidate and remove the least frequently used key before inserting a new item. For this problem, when there is a tie (i.e., two or more keys with the same frequency), the least recently used key would be invalidated.

To determine the least frequently used key, a use counter is maintained for each key in the cache. The key with the smallest use counter is the least frequently used key. When a key is first inserted into the cache, its use counter is set to 1¹. The use counter for a key in the cache is incremented either a get or put operation is called on it. The functions get and put must each run in $\Theta(1)$ time complexity.

import java.util.HashMap;
import java.util.LinkedHashSet;

class LFUCache {
  int capacity;
  HashMap<Integer, Integer> cache;
  HashMap<Integer, Integer> key_count;
  HashMap<Integer, LinkedHashSet<Integer>> count_keys;
  int min;

  public LFUCache(int capacity) {
    this.capacity = capacity;
    cache = new HashMap<>();
    key_count = new HashMap<>();
    count_keys = new HashMap<>();
    count_keys.put(1, new LinkedHashSet<>());
  }
  
  public int get(int key) {
    if (cache.containsKey(key)) {
      int count = key_count.get(key);
      count_keys.get(count).remove(key);
      if (count == min && count_keys.get(count).isEmpty()) min++;
      key_count.put(key, ++count);
      count_keys.computeIfAbsent(count, x -> new LinkedHashSet<>()).add(key);
      return cache.get(key);
    }
    return -1;
  }
  
  public void put(int key, int value) {
    if (cache.containsKey(key)) {
      get(key);
      cache.put(key, value);
      return;
    }
    else if (cache.size() >= capacity) {
      int lfu = count_keys.get(min).iterator().next();
      cache.remove(lfu);
      key_count.remove(key);
      count_keys.get(min).remove(lfu);
    }
    cache.put(key, value);
    key_count.put(key, 1);
    count_keys.get(1).add(key);
    min = 1;
  }
}

Random Pick with Blacklist

You are given an integer n and an array of unique integers blacklist. Design an algorithm to pick a random integer in the range [0, n - 1] that is not in blacklist. Any integer that is in the mentioned range and not in blacklist should be equally likely to be returned. Optimize your algorithm such that it minimizes the number of calls to the built-in random function of your language.

Implement the Solution class:

• Solution(int n, int[] blacklist) Initializes the object with the integer n and the blacklisted integers blacklist.
• int pick() Returns a random integer in the range [0, n - 1] and not in blacklist.

import java.util.HashMap;
import java.util.Map;
import java.util.Random;

class Solution {
  Map<Integer, Integer> integerIndex;
  int m;
  Random random;

  public Solution(int n, int[] blacklist) {
    integerIndex = new HashMap();
    for (int x : blacklist) integerIndex.put(x, 1);
    m = n - integerIndex.size();
    for (int x : blacklist) if (x < m) {
      while (integerIndex.containsKey(n - 1)) n--;
      integerIndex.put(x, --n);
    }
    random = new Random();
  }
  
  public int pick() {
    int x = random.nextInt(m);
    return integerIndex.containsKey(x) ? integerIndex.get(x) : x;
  }
}

How to Test Your Code

Corner Cases and Edge Cases

String to Integer (atoi)

Implement the myAtoi(string s) function, which converts a string to a 32-bit signed integer. The algorithm for myAtoi(string s) is as follows:

1. Whitespace: Ignore any leading whitespace (" ").
2. Signedness: Determine the sign by checking if the next character is '-' or '+', assuming positivity if neither present.
3. Conversion: Read the integer by skipping leading zeros until a non-digit character is encountered or the end of the string is reached. If no digits were read, then the result is 0.
4. Rounding: If the integer is out of the 32-bit signed integer range [-2^31, 2^31 - 1], then round the integer to remain in the range. Specifically, integers less than -2^31 should be rounded to -2^31, and integers greater than 2^31 - 1 should be rounded to 2^31 - 1.

Return the integer as the final result.

#include <climits>
#include <string>

int div = INT_MAX / 10, mod = INT_MAX % 10;

int myAtoi(std::string s) {
  int i, sign = 1, integer = 0;
  for (i = 0; s[i] == ' '; i++);
  if (s[i] == '-') {
    sign = -1;
    i++;
  }
  else if (s[i] == '+') i++;
  while ('0' <= s[i] && s[i] <= '9') {
    int digit = s[i++] - '0';
    if (integer > div || integer == div && digit > mod)
      return sign == 1 ? INT_MAX : INT_MIN;
    integer = integer * 10 + digit;
  }
  return sign * integer;
}

Valid Number

Given a string s, return whether s is a valid number. For example, all the following are valid numbers: ["2", "0089", "-0.1", "+3.14", "4.", "-.9", "2e10", "-90E3", "3e7", "-6e-1", "53.5e93", "-123.456e789"], while the following are not valid numbers: ["abc", "1a", "1e", "e3", "99e2.5", "--6", "-+3", "95a54e53"]. Formally, a valid number is defined using one of the following definitions:

1. An integer number followed by an optional exponent.
2. A decimal number followed by an optional exponent.

An integer number is defined with an optional sign (- or +) followed by digits. A decimal number is defined with an optional sign (- or +) followed by one of the following definitions:

1. Digits followed by a dot (.).
2. Digits followed by a dot (.) followed by digits.
3. A dot (.) followed by digits.

An exponent is defined with an exponent notation (e or E) followed by an integer number. The digits are defined as one or more digits.

def isNumber(s):
    digits, dot, e, exponent = False, False, False, True
    for i, x in enumerate(s):
        if x.isdigit(): digits = exponent = True
        elif x == '.':
            if dot or e: return False
            dot = True
        elif x.lower() == 'e':
            if not digits or e: return False
            e, exponent = True, False
        elif x not in '-+' or i and s[i - 1].lower() != 'e': return False
    return digits and exponent

Strong Password Checker

A password is considered strong if the below conditions are all met:

• It has at least 6 characters and at most 20 characters.
• It contains at least one lowercase letter, at least one uppercase letter, and at least one digit.
• It does not contain three repeating characters in a row².

Given a string password, return the minimum number of steps required to make password strong. If password is already strong, return 0.

In one step, you can:

• Insert one character to password,
• Delete one character from password, or
• Replace one character of password with another character.

int strongPasswordChecker(string password) {
  bool lowercase = true, uppercase = true, digit = true;
  for (char x : password) {
    if (islower(x)) lowercase = false;
    else if (isupper(x)) uppercase = false;
    else if (isdigit(x)) digit = false;
  }
  int n = password.size(), mod[3], counter[3];
  for (int i = 2; i < n; i++)
    if (password[i - 2] == password[i] && password[i - 1] == password[i]) {
      int j;
      for (j = 3; i + 1 < n && password[i] == password[i + 1]; i++, j++);
      mod[j % 3]++;
      counter[0] += j / 3;
    }
  int contain = lowercase + uppercase + digit;
  if (n < 6) return max(contain, 6 - n);
  else if (n <= 20) return max(contain, counter[0]);
  else {
    counter[1] = n - 20;
    counter[2] = min(counter[1], mod[0]);
    counter[0] -= counter[2];
    counter[1] -= counter[2];
    counter[2] = min(counter[1], mod[1] * 2) / 2;
    counter[1] -= counter[2] * 2;
    return n + max(contain, counter[0] - counter[1] / 3 - counter[2]) - 20;
  }
}

LFU Cache

Design and implement a data structure for a Least Frequently Used (LFU) cache.

Implement the LFUCache class:

• LFUCache(int capacity) initializes the object with the capacity of the data structure.
• int get(int key) gets the value of the key if the key exists in the cache. Otherwise, returns -1.
• void put(int key, int value) updates the value of the key if present, or inserts the key if not already present. When the cache reaches its capacity, it should invalidate and remove the least frequently used key before inserting a new item. For this problem, when there is a tie³, the least recently used key would be invalidated.

To determine the least frequently used key, a use counter is maintained for each key in the cache. The key with the smallest use counter is the least frequently used key. When a key is first inserted into the cache, its use counter is set to 1⁴. The use counter for a key in the cache is incremented either a get or put operation is called on it. The functions get and put must each run in $\Theta(1)$ average time complexity.

import java.util.HashMap;
import java.util.LinkedHashSet;

class LFUCache {
  int capacity;
  HashMap<Integer, Integer> cache;
  HashMap<Integer, Integer> key_count;
  HashMap<Integer, LinkedHashSet<Integer>> count_keys;
  int min;

  public LFUCache(int capacity) {
    this.capacity = capacity;
    cache = new HashMap<>();
    key_count = new HashMap<>();
    count_keys = new HashMap<>();
    count_keys.put(1, new LinkedHashSet<>());
  }
  
  public int get(int key) {
    if (cache.containsKey(key)) {
      int count = key_count.get(key);
      count_keys.get(count).remove(key);
      if (count == min && count_keys.get(count).isEmpty()) min++;
      key_count.put(key, ++count);
      count_keys.computeIfAbsent(count, x -> new LinkedHashSet<>()).add(key);
      return cache.get(key);
    }
    return -1;
  }
  
  public void put(int key, int value) {
    if (cache.containsKey(key)) {
      get(key);
      cache.put(key, value);
      return;
    }
    else if (cache.size() >= capacity) {
      int lfu = count_keys.get(min).iterator().next();
      cache.remove(lfu);
      key_count.remove(key);
      count_keys.get(min).remove(lfu);
    }
    cache.put(key, value);
    key_count.put(key, 1);
    count_keys.get(1).add(key);
    min = 1;
  }
}