Linear Systems
import numpy as np
import math
Mole/Mass Balance
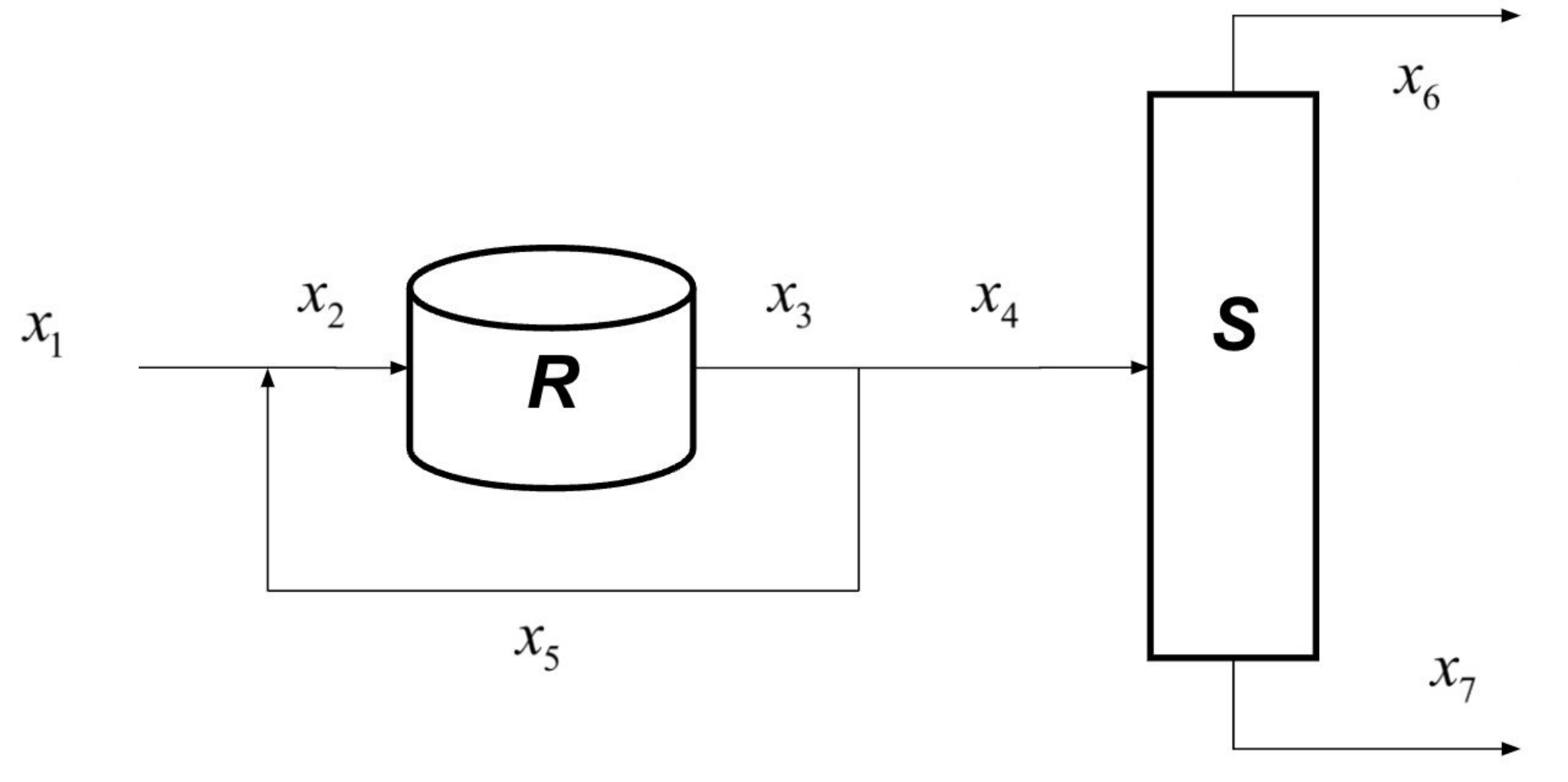
Set up the mole balance equations for this PFD, given that \(R\), \(S\) operate so \(x_3 = R x_2\) and \(x_6 + x_7 = S x_4\). Then arrange in the form \(Ax = b\).
\[\begin{bmatrix} -1 & 1 & 0 & 0 & -1 & 0 & 0 \\ 0 & -R & 1 & 0 & 0 & 0 & 0 \\ 0 & 0 & 1 & -1 & -1 & 0 & 0 \\ 0 & 0 & 0 & S & 0 & -1 & -1 \\ \end{bmatrix} \begin{bmatrix} x_1 \\ x_2 \\ x_3 \\ x_4 \\ x_5 \\ x_6 \\ x_7 \\ \end{bmatrix} = \begin{bmatrix} 0 \\ 0 \\ 0 \\ 0 \\ \end{bmatrix}\]Write a function my_make_lin_ind(A), where A and B are matrices. Let the rank(A) = n. Then B should be a matrix containing the first n columns of A that are all linearly independent. Note that this implies that B is full rank.
import copy
from math import isclose
def my_make_lin_ind(A):
B = []
for jA in range(len(A[0])):
B.append(A[:, jA])
n, m = len(B), len(B[0])
C = copy.deepcopy(B)
for i in range(n):
if isclose(C[i][i], 0):
for jC in range(i + 1, n):
if not isclose(C[jC][i], 0):
C[i], C[jC] = C[jC], C[i]
break
if isclose(C[i][i], 0):
continue
for jC in range(i + 1, n):
x = C[jC][i] / C[i][i]
for k in range(i, m):
C[jC][k] -= x * C[i][k]
if sum(any(row) for row in C) != len(B):
B.pop()
return list(zip(*B))
## Test cases
A = np.array([[12,24,0,11,-24,18,15],
[19,38,0,10,-31,25,9],
[1,2,0,21,-5,3,20],
[6,12,0,13,-10,8,5],
[22,44,0,2,-12,17,23]])
B = my_make_lin_ind(A)
# B = [[12,11,-24,15],
# [19,10,-31,9],
# [1,21,-5,20],
# [6,13,-10,5],
# [22,2,-12,23]]
print(B)
[(12, 11, -24, 18, 15), (19, 10, -31, 25, 9), (1, 21, -5, 3, 20), (6, 13, -10, 8, 5), (22, 2, -12, 17, 23)]
\(Ly = b\)
Solve for \(y\) if \(Ly = b\). It should only take O(\(n^2\)) \(\approx\) 9 flops.
\[\begin{array}{|l|l|} \hline L = \begin{bmatrix} 1 & 0 & 0 \\ 2 & 4 & 0 \\ 5 & 2 & 3 \\ \end{bmatrix} & b = \begin{bmatrix} 0 \\ 4 \\ 6 \\ \end{bmatrix} \\ \hline L = \begin{bmatrix} 1 & 0 & 0 \\ 0 & 4 & 0 \\ 5 & 2 & 3 \\ \end{bmatrix} & b = \begin{bmatrix} 0 \\ 4 \\ 6 \\ \end{bmatrix} \\ \hline L = \begin{bmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 5 & 2 & 3 \\ \end{bmatrix} & b = \begin{bmatrix} 0 \\ 1 \\ 6 \\ \end{bmatrix} \\ \hline L = \begin{bmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 2 & 3 \\ \end{bmatrix} & b = \begin{bmatrix} 0 \\ 1 \\ 6 \\ \end{bmatrix} \\ \hline L = \begin{bmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 3 \\ \end{bmatrix} & b = \begin{bmatrix} 0 \\ 1 \\ 4 \\ \end{bmatrix} \\ \hline L = \begin{bmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \\ \end{bmatrix} & b = \begin{bmatrix} 0 \\ 1 \\ \frac{4}{3} \\ \end{bmatrix} \\ \end{array}\]Vector Norms
one_norm = lambda vector: sum(sum(abs(column) for column in row) for row in vector)
two_norm = lambda vector: math.sqrt(sum(sum(column**2 for column in row) for row in vector))
infinity_norm = lambda vector: max(max(abs(column) for column in row) for row in vector)
Find the 1-norm, 2-norm (Euclidean norm), and the infinity-norm of the following vectors:
x = [[1], [4], [9], [1], [15]]
y = [[2], [0], [-7], [0], [0]]
print(f'x: 1-norm = {one_norm(x)}, 2-norm = {two_norm(x)}, infinity-norm = {infinity_norm(x)}')
print(f'y: 1-norm = {one_norm(y)}, 2-norm = {two_norm(y)}, infinity-norm = {infinity_norm(y)}')
x: 1-norm = 30, 2-norm = 18.0, infinity-norm = 15
y: 1-norm = 9, 2-norm = 7.280109889280518, infinity-norm = 7
Given the linear system
\[2x_1 - 6 \alpha x_2 = 3\] \[3 \alpha x_1 - x_2 = \frac{3}{2}\]-
Find value(s) of \(\alpha\) for which the systems has no solutions.
\[2 (-1) = -6 \alpha \cdot 3 \alpha\] \[-2 = -18 \alpha^2\] \[\frac{1}{9} = \alpha^2\] \[\alpha = \pm \frac{1}{3}\] \[2x_1 + 6 \frac{1}{3} x_2 = 2x_1 + 2x_2\] \[-3 \frac{1}{3} x_1 - x_2 = -x_1 - x_2\] \[\frac{2}{-1} \neq 3 \div \frac{3}{2}\] \[\alpha = -\frac{1}{3}\] -
Find value(s) of \(\alpha\) for which the systems has an infinite number of solutions.
\[2x_1 - 6 \frac{1}{3} x_2 = 2x_1 - 2x_2\] \[3 \frac{1}{3} x_1 - x_2 = x_1 - x_2\] \[\frac{2}{1} = 3 \div \frac{3}{2}\] \[\alpha = \frac{1}{3}\] -
Assuming a unique solution exists for a given \(\alpha\) find the solution.
Compute the eigenvalues and associated eigenvectors of the following matrix.
\[\begin{bmatrix} 0 & 1 \\ 1 & 1 \\ \end{bmatrix}\] \[\begin{vmatrix} -\lambda & 1 \\ 1 & 1 - \lambda \\ \end{vmatrix} = \lambda^2 - \lambda - 1 = 0\] \[\lambda = \frac{1 \pm \sqrt{1^2 + 4 \cdot 1 \cdot 1}}{2 \cdot 1} = \frac{1 \pm \sqrt{5}}{2}\] \[\begin{bmatrix} -\lambda & 1 \\ 1 & 1 - \lambda \\ \end{bmatrix} = \begin{bmatrix} 0 \\ 0 \\ \end{bmatrix}\] \[\begin{bmatrix} 1 & 0 \\ 0 & 1 \\ \end{bmatrix} = \begin{bmatrix} \lambda \\ \lambda (\lambda - 1) \\ \end{bmatrix}\]sqrt5 = math.sqrt(5)
eigenvalue = np.array([(1 - sqrt5) / 2, (1 + sqrt5) / 2])
eigenvector = np.array([eigenvalue * (eigenvalue - 1), eigenvalue])
print(f'eigenvalue = {eigenvalue[0]}, eigenvector = {eigenvector[:, 0].T}')
print(f'eigenvalue = {eigenvalue[1]}, eigenvector = {eigenvector[:, 1].T}')
eigenvalue = -0.6180339887498949, eigenvector = [ 1. -0.61803399]
eigenvalue = 1.618033988749895, eigenvector = [1. 1.61803399]