Root Finding
import math
Bisection
# def f(x):
# ...
def bisect(lo, hi, tolerance):
if math.isclose(lo, 0):
return lo
elif math.isclose(hi, 0):
return hi
f_lo, f_hi = map(f, (lo, hi))
if f_lo < 0 < f_hi:
is_increasing = True
elif f_hi < 0 < f_lo:
is_increasing = False
else:
raise ValueError
while not math.isclose(lo, hi, abs_tol=tolerance):
mid = (lo + hi) / 2
if (f(mid) > 0) ^ is_increasing:
lo = mid
else:
hi = mid
return lo
Consider the problem of building a pipeline from an offshore oil platform, a distance H miles from the shoreline, to an oil refinery station on land, a distance L miles along the shore. The cost of building the pipe is C_ocean while the pipe is under the ocean and C_land while the pipe is on land. The pipe will be built in a straight line toward the shore where it will make contact at some point, x between 0 and L. It will continue along the shore on land until it reaches the oil refinery. See the figure for clarification.
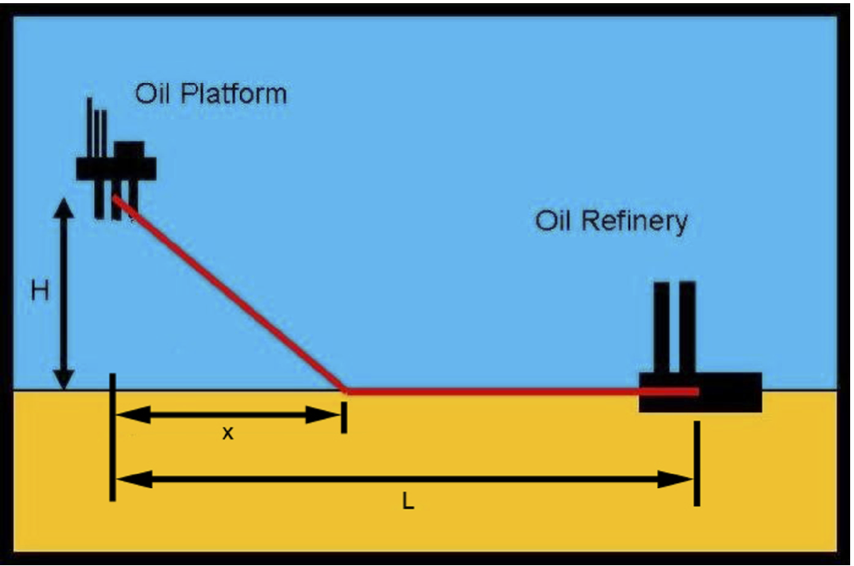
Write a function my_pipe_builder(C_ocean, C_land, L, H), where the input arguments are as described earlier, and \(x\) is the x-value that minimizes the total cost of the pipeline. You should use the bisection method to determine this value to within a tolerance of 1e-6 starting at an initial bound of \(a = 0\) and \(b = L\).
Test Cases:
In: my_pipe_builder(20, 10, 100, 50)
Out: 28.867512941360474
In: my_pipe_builder(30, 10, 100, 50)
Out: 17.677670717239380
In: my_pipe_builder(30, 10, 100, 20)
Out: 7.071067392826080
def my_pipe_builder(C_ocean, C_land, L, H, tolerance=1e-6):
a, b = 0, L
cost = lambda x: C_ocean * math.sqrt(H**2 + x**2) + C_land * (L - x)
while not math.isclose(a, b, abs_tol=tolerance):
x = (a + b) / 2
if cost(x - tolerance) < cost(x + tolerance):
b = x
else:
a = x
return x
print(my_pipe_builder(20, 10, 100, 50))
print(my_pipe_builder(30, 10, 100, 50))
print(my_pipe_builder(30, 10, 100, 20))
28.867513686418533
17.67766997218132
7.07106813788414
Newton-Raphson
def newtonRaphson(x, tolerance, f_prime=None):
previous = float('inf')
while not math.isclose(previous, x, abs_tol=tolerance):
y = f(x)
y_prime = (f(x + tolerance) - f(x - tolerance)) / tolerance / 2 if f_prime is None else f_prime(x)
previous = x
x -= y / y_prime
return x
Use Newton’s method to find a solution accurate to within \(10^{-4}\).
\(x - \cos x = 0\) on \([0, \frac{\pi}{2}]\)
previous = float('inf')
x = (0 + math.pi) / 2
while not math.isclose(previous, x, abs_tol=10e-4):
y = x - math.cos(x)
y_prime = 1 + math.sin(x)
previous = x
x -= y / y_prime
print(x)
0.7390851781060102